基于改进麻雀算法的骨折复位机器人控制器优化

容摘要

骨折复位机器人（fracture reduction robot，FRR）的精度是影响复位手术安全性的重要因素。本文提出了一种基于Levy flight算子的麻雀搜索算法Levy-SSA，用于机器人控制器参数的自整定，以提高FRR的复位精度，实现更加安全、稳定的复位运动。本研究首先对FRR进行逆运动学分析，利用Simulink建立机器人动力学模型，结合计算力矩法设计FRR逆动力学控制器；然后通过仿真实验和实物实验得到执行机构驱动杆实际杆长变化与期望杆长变化的误差。与传统未优化的控制器相比，经Levy-SSA优化后的FRR复位误差总体上降低了2个数量级，平均降低了98.74%。

 

（一）FRR系统基于Stewart平台搭建，由并联机构、扫描环、抱闸模块、限位开关、可调节双目相机、电气模块、克氏针及泰勒环组成，其三维模型及实物如图1所示。FRR能实现6个自由度的平移、旋转运动，6根连杆采用无刷直流电机（BLDC）搭配滚珠丝杠，可以把电机的转动运动变成连杆的直线运动。这种方式控制精度高，且启动力矩非常小，可以实现微给进运动。针对骨折，中医手法正骨过程主要包括拔伸牵引、旋转屈伸和端挤提按，Stewart平台可以通过规划机器人运动轨迹模拟中医复位手法。

 

图1 FRR三维模型及实物图

 

FRR的工作流程如下：①将远端和近端断骨利用克氏针固定在平台上，然后利用双目相机进行标定，建立世界坐标系，结合医学影像实现三维重建，并通过视觉系统测量远端骨骼和近端骨骼的相对位姿；②通过上位机软件计算动平台期望位姿，并将位姿解算为期望驱动杆长度和速度信号，输入给末端执行器进行复位运动，经过一系列平移、旋转运动使断骨面对齐；③通过骨外固定器进行固定，完成复位。

 

（二）控制器参数是影响FRR复位精度的重要因素，合适的PID参数能够有效减少实际位姿与期望位姿的误差。与传统方法在FRR控制器参数整定性能上相比，智能优化算法在保证系统动态特性、稳态误差和抗干扰性等方面具有优势，同时降低了人力参与程度。

 

Levy-SSA与传统SSA的搜索能力对比如图7所示，左侧展示了Levy-SSA的参数空间，右侧展示了SSA和Levy-SSA的迭代次数与最佳自适应值的关系。

 

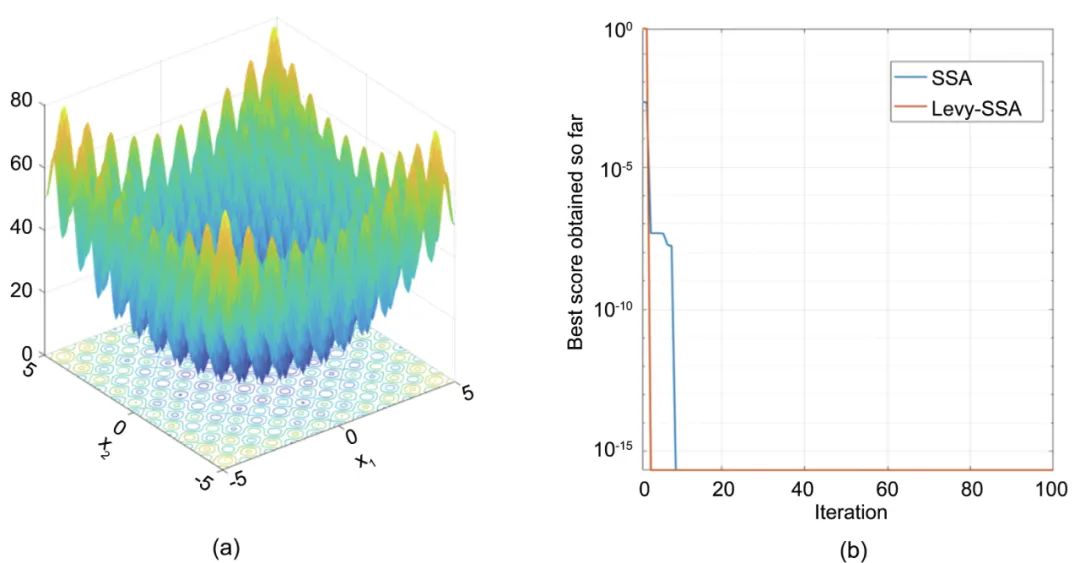
图7 Levy-SSA与传统SSA搜索能力对比

 

如图8所示，与SSA、粒子群优化算法、遗传算法、鲸鱼优化算法和人工蜂鸟算法相比，Levy-SSA的收敛速度和全局搜索能力更有优势。

 

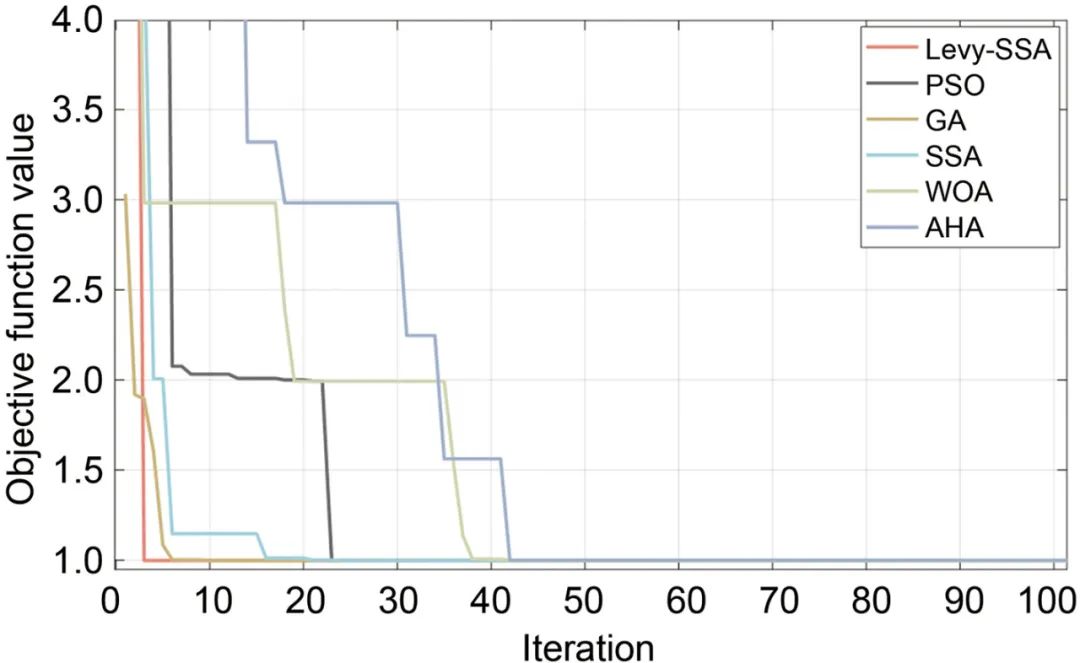
图8 不同算法的优化性能比较

 

（三）基于计算力矩法的FRR控制系统整体架构如图9所示。将期望轨迹输入FRR系统，经过逆运动学模块将期望位姿解算为期望杆长，其与实际输出杆长的偏差e(t)作为控制器的输入，控制器的输出是关节驱动力，控制FRR执行器进行复位运动，最后经过正向运动学模块将关节位移、平台位姿以及速度转化为机器人的实际运动轨迹。为了模拟FRR的工作环境，系统引入扰动扭力F_d模拟软组织对机构的阻力，使仿真结果更加贴近实际情况。

 

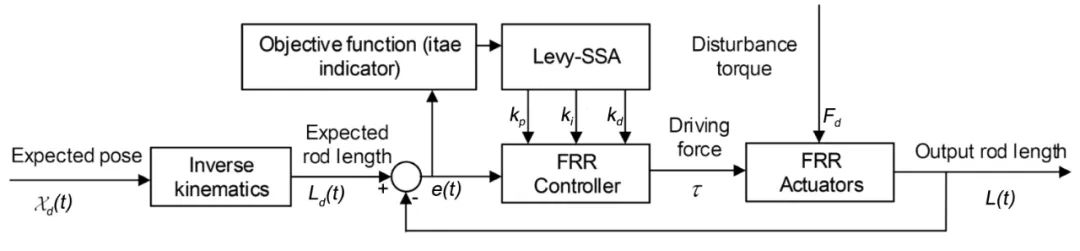
图9 FRR控制系统整体架构

 

（四）仿真实验中，Levy-SSA算法在每次运行迭代的过程中对控制器参数K_p、K_i、K_d进行寻优调整。目标函数计算每次调整的适应度值，然后进行下一次迭代运行，继续寻优，直到迭代次数达到预设要求。

 

基于Simulink构建的FRR动力学模型如图10所示。

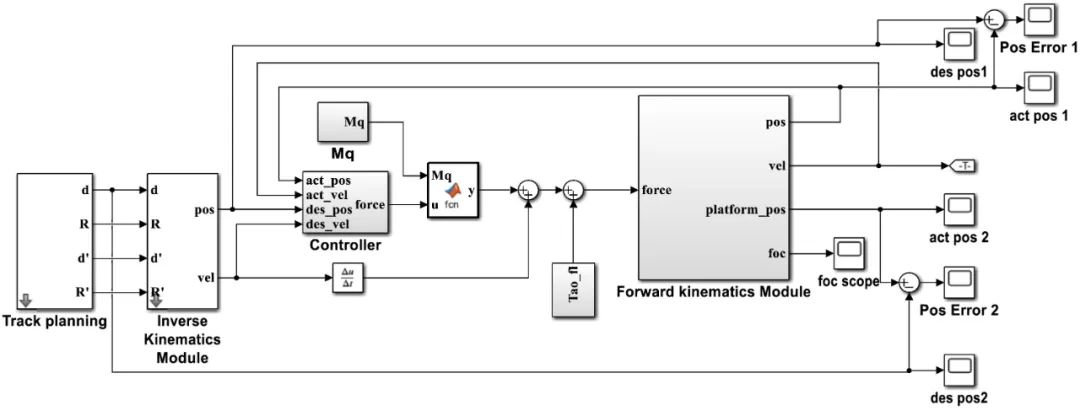
图10 FRR动力学模型

 

图11展示了增加Levy-SSA算法优化PID参数的FRR控制器。

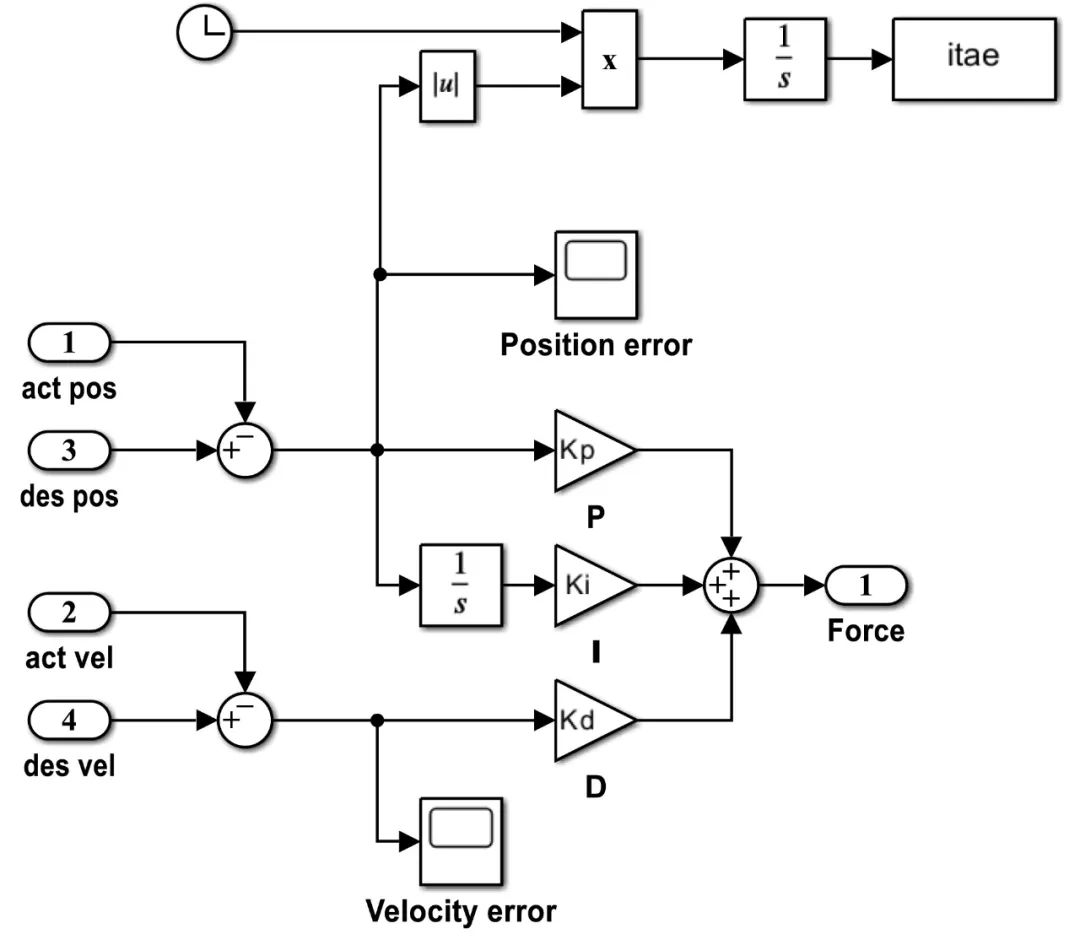
图11 FRR控制器模块

 

（四）仿真实验中，设置种群数量为100，迭代次数为100次，控制器参数K_p、K_i、K_d的搜索上界和下界分别为4000、4000、50和0.01、0.01、0.01。参数设置完毕后进行仿真分析，将设定好的期望位姿输入到FRR轨迹规划模块。具体位姿如表1所示。

 

表1 FRR机构的初始位置和期望位置

经过100次系统搜索迭代，得到的Levy-SSA对FRR的最佳适应变化曲线如图12所示。

 

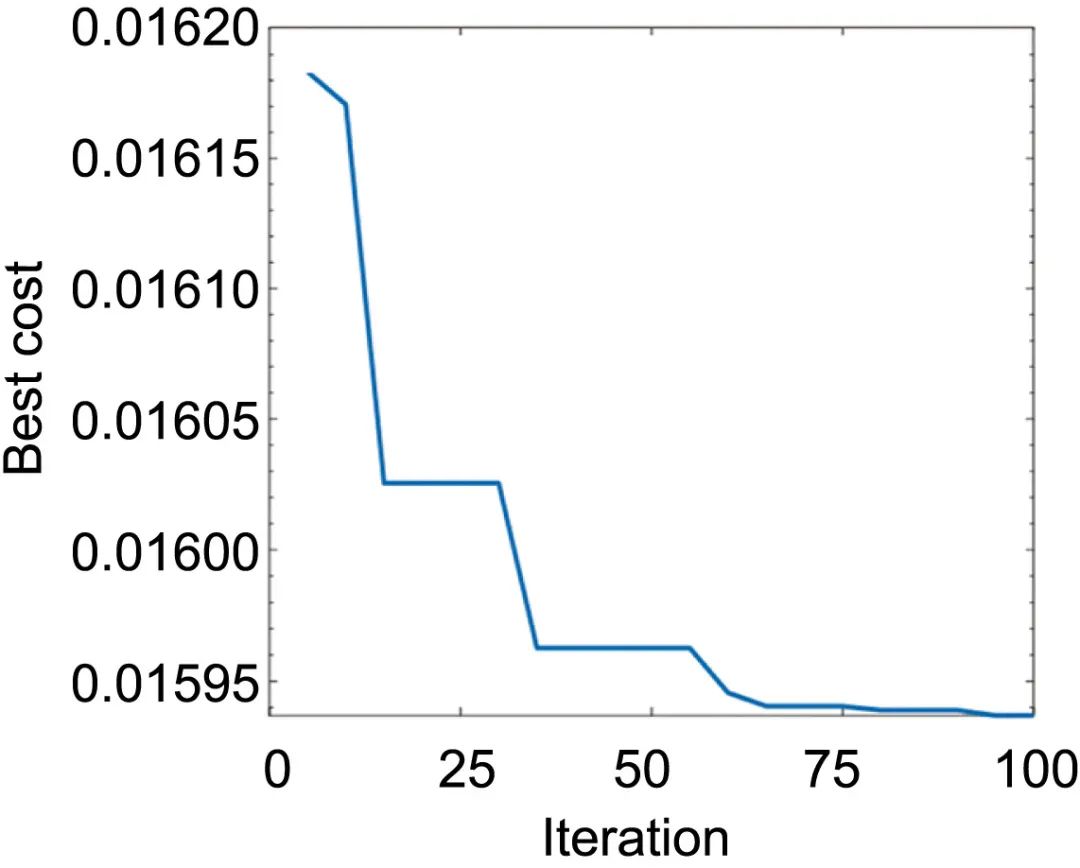
图12 Levy-SSA算法在FRR上的适应度变化曲线

 

在100次迭代过程中，适应度值显著下降，算法的优化搜索过程相对平稳。图17和图15分别展示了通过Levy-SSA优化前后，6根驱动杆长度变化误差。

 

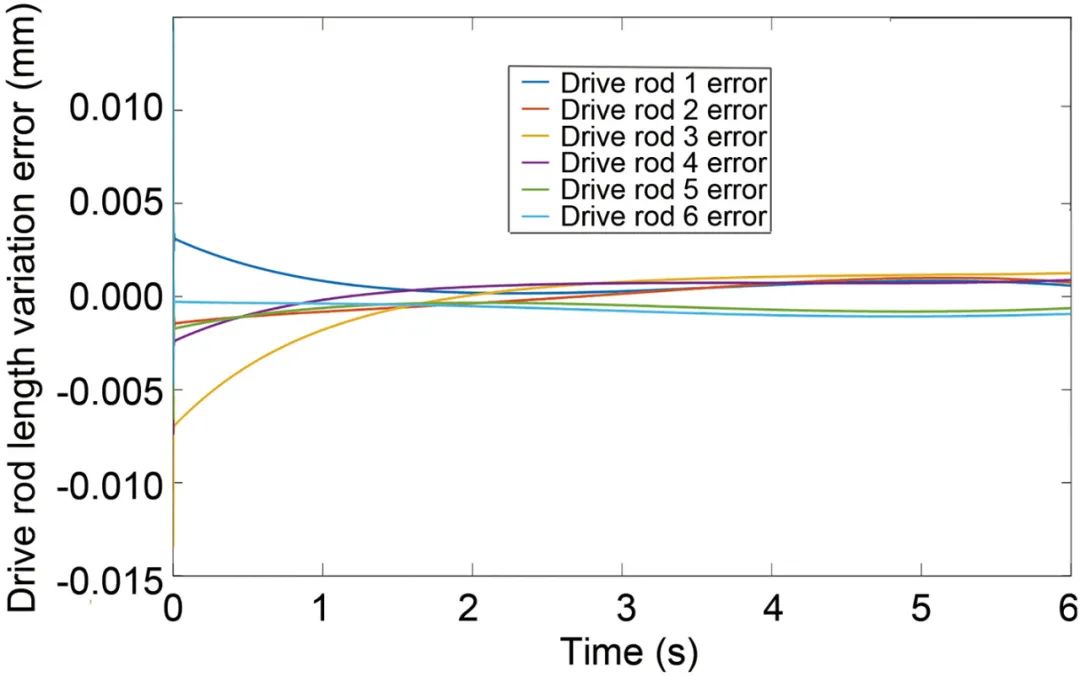
图15  Levy-SSA算法优化后各杆长变化误差曲线

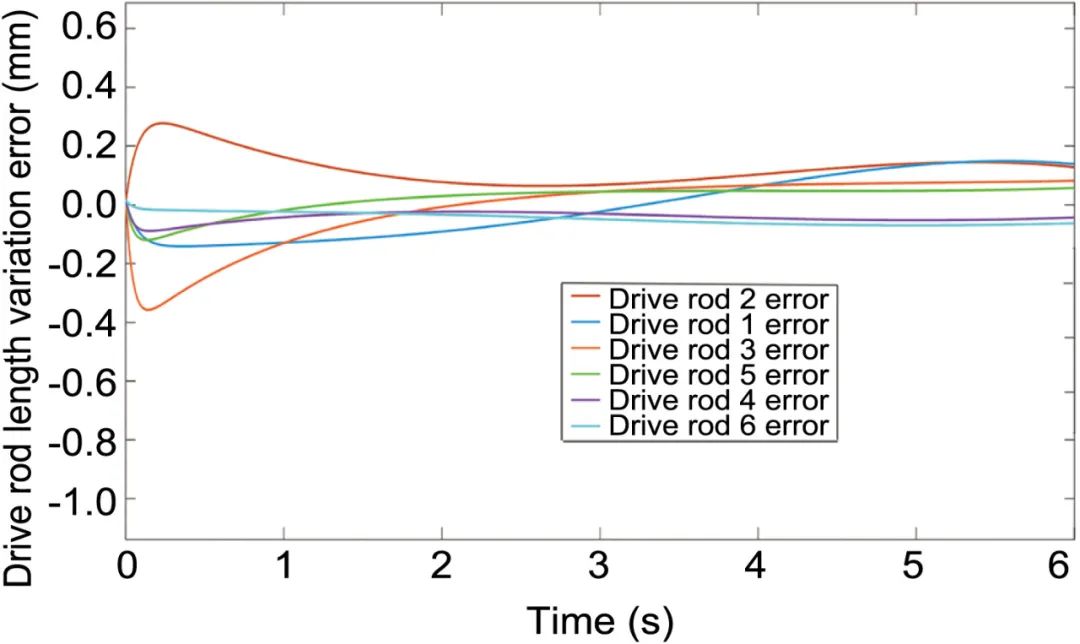
图17 优化前各杆长变化误差曲线

 

6根驱动杆的长度变化直接影响移动平台的位置变化，移动平台的期望位置与实际位置之间的误差决定了FRR的精度。将Levy-SSA应用于FRR控制器参数自整定，优化后的参数范围内的杆长误差显著减小，这表明PID参数范围的设置与算法的参数设置相匹配，并且这对于裂缝减少系统可以满足迭代次数设置要求。

 

（五）分别开展了使用Levy-SSA优化前和优化后的FRR还原物体的实验。优化前后的复位过程分别如图20和图21所示。将杆长变化数据记录在上位机中，计算出与预期杆长变化数据的差值。6根驱动杆平均误差减少了98.74%，机器人减速精度显著提高。

 

图20 优化前的FRR实物复位图

图21 优化后的FRR实物复位图

 

骨折复位是一项对精度要求高的手术，由于机器人的刚性结构，即使是轻微的错误也会对患者造成不可逆转的继发性伤害。本文提出的Levy-SSA 算法加速了骨折复位机器人控制系统收敛到最优解，提高了运动轨迹的精度，对机器人控制器优化具有重要意义。

 

【作者信息】

Baichuan An^a,*, Jianwen Chen^b, Hao Sun^a,c,*, Minghuan Yin^a, Zicheng Song^a, Chao Zhuang^a, Cheng Chang^a, Minghe Liu^a

a School of Artificial Intelligence and Data Science, Hebei University of Technology, Tianjin 300401, China

b Limb Deformity Correction and Function Reconstruction Department, Southern University of Science and Technology Hospital, Shenzhen 518000, China‍

c Engineering Research Center of Intelligent Rehabilitation Device and Detection Technology, Ministry of Education, Tianjin 300401, China

* Author to whom correspondence should be addressed: sunhao@hebut.edu.cn