(上接2月刊)
尺寸偏差分析的方法
偏差分析基于两种假设,假设条件分为刚性假设分析法和柔性假设分析法两种。
1、刚性装配偏差分析
刚性假设是不考虑零件的弹塑性变形,仅考虑零件整体的平移和旋转,一般采用运动学分析理论。目前,在尺寸公差优化设计领域,常用的方法有三种:极值法、概率法和统计试验法。极值法是按照完全互换法设计尺寸及公差,计算量小、理论简单,但是由于所有零件的公差同时处于极值的可能性很小,因此这种方法通常适用于具有较小公差带的情况。概率法是假定各零件尺寸公差服从正态分布,装配公差与零件公差之间是线性关系,使得实际情况得到简化,建模过程也接近实际,但是一旦假设不成立,这种方法无法模拟实际。统计试验法是通过随机变量的统计试验、随机模拟,求解数学物理、工程技术问题近似解的数值方法,这种方法在实际工程应用中较为广泛。
1.1极值法
极值法的特点就是零件偏差位于公差带的边界上,假设装配过程中各零件的尺寸均处于极限状态,这种方法一般用于线性问题。极值分析方法能够保证所有偏差累积后不会超过公差所要求的范围。多用于组成环较少或者要保证完全互换的情况。对于线性尺寸链,可以从极值法的公式中推导出公差函数;对于非线性尺寸链,公差函数没有统一的表达式,要根据尺寸链的几何关系确定。假设装配过程各个零件均符合正态分布,其计算方法如下:
1.2均方根法
均方根发也称作统计法,假设各个零件的公差服从正态分布,装配工差与零件公差是线性关系,能够有效地分析一维装配偏差和二维刚体装配简单情况。目前此方法在轿车零件的公差设计中应用广泛,多应用在组成环环数多的情况。
根据分布特性进行封闭环和组成环公差的分析方法称为统计法。为了便于描述,需要线对公差函数进行定义。公差函数是尺寸链中欲求解封闭环或组成环与已知组成环和封闭环函数关系的表达式,设公差函数为:
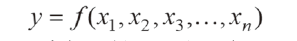
(1)
式中,y为欲求解的封闭环或组成环的尺寸及偏差;凡为已知组成环和封闭环的个数;为相瓦独立的已知的组成环和封闭环的尺寸及偏差。
1.3蒙特卡洛法
蒙特卡洛法又称为概率模拟法或者随机抽样技术,蒙特卡罗算法的基本思想为当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。用蒙特卡罗算法求解公差问题,就是把求封闭环尺寸公差的问题转化为求解一个随机变量的统计问题来处理;封闭环尺寸公差的确定,采用随机模拟和统计实验的方法求解,用这种方法得到的结果比较符合实际情况。
蒙特卡洛的思路为:首先根据零件尺寸的实际分布由计算机生成一组伪随机数,然后将伪随机数代入偏差模型计算一系列的尺寸值,最后计算尺寸的各阶中心距,拟出尺寸近似的分布。它是一种随机模拟,统计验证来求解近似解的数值方法。能够基于各零件的具体特征准确地对公差设计的合力性进行分析。
以上三种装配偏差方法以及目前主流分析软件的共同特点都是以刚体零件为研究对象,其装配偏差的统计特征由零件几何与运动关系确定。
2、柔性装配偏差分析法
柔性偏差分析法假设条件须考虑零件装配变形,一般引入弹塑性力学理论。由于车身零件为金属薄板件,在装配过程中易变形,应用刚性假设在车身尺寸分析中误差较大,近年来针对车身零件的刚性假设尺寸偏差研究已经逐渐减少。对于柔性假设的车身薄板件装配偏差分析的研究,目前具有代表性的研究成果包括:影响系数法、有限元法、柔性静态分析法和功平衡法。
2.1影响系数法
密歇根大学的Liu在1995年提出一维悬臂梁偏差分析结构,该结构将板厚和夹具初始偏差作为分析变量,来研究焊接后偏差。研究结论:(a)夹具偏差较小时且板厚相同时,装配偏差最小;(b)较厚板对装配偏差影响较大;(c)夹具偏差较大时,板厚相差越大则装配偏差越小。
密歇根大学的Hu(Hushixing)在1997年提出偏差流(SOV,SteamofVariation)理论,该理论将零件结构分析和统计分析相结合,定性研究串行装配和并行装配的偏差传递关系。该方法仅从定性层面对偏差进行诊断,未能提供定量和误差方差的诊断策略。
密歇根大学的Liu和Hu于1997年在SOV理论的基础上,提出能够分析柔性薄板件装配偏差的影响系数法。该方法是通过有限元分析建立零件与装配体之间的力学偏差模型,如式(2)所示:
U=S·V (2)
模型中输入蒙特卡洛模拟偏差,得到装配偏差的统计分布结果。该方法提高了计算效率,克服了在有限元分析基础上利用蒙特卡洛方法计算量大的问题。
Liu和Hu于1998年在影响系数法基础上,研究了对接、角接、搭接三种焊接接头结构对装配偏差的影响并设计三种接头的盒形结构进行试验。结果表明:搭接接头尺寸质量最好,其次是角接,最后是对接。
Volvo公司的Dahlstom等在2002年利用实例分析了焊接顺序和焊接类型对装配偏差的影响。但运用有限元进行焊接仿真复杂且需要丰富的经验,即在偏差分析中该方法不可取。2004年Dahlstom在影响系数法基础上,研究了接触模型对装配偏差的影响。
文中考虑到在焊接模拟仿真中,零件主面和从面相互穿透的问题,并分析了装配偏差传递流程,提出解决接触穿透的平衡矩阵方法。2009年Ungemach也针对接触不穿透问题进行了相应的研究。上海交通大学的胡敏根据有限元分析理论和ANSYS软件提出了基于接触模型的车身薄板装配偏差研究的模拟方法。该方法在对薄板件点焊热分析的基础上建立适用于柔性薄板件装配偏差分析的有限元模型,研究了装配体偏差源和点焊顺序对装配变形的影响。
2.2有限元方法
1997年,通用技术中心的Hsieh等提出了一种对柔性薄板件装配和优化的有限元分析模型。该模型将装配过程划分为:夹持、焊接和释放,并利用几何算法模拟焊点在焊接过程中的偏移。
在该模型基础上,结合计算机数据库技术,设计出针对柔性薄板件偏差分析的EVAS软件。2002年,Xie在EVAS软件基础上,利用智能优化算法对零件夹持和焊接顺序进行优化。
2.3变形云图优化分析推演法
目前,白车身制造误差的诊断方法不能获得百分之百的产品质量检验数据,而且诊断耗时长,往往诊断出的误差已经传至下一工序,难以准确及时评价车身焊装质量。变形云图优化分析推演法为解决白车身制造误差诊断的新方法,与统计分析方法不同,该方法利用ANSYS有限元分析,将变形量和变形趋势准确地定量及定性反映在计算机的数学模型上,得到变形云图,并以黄金分割法和主方向法等优化理论为辅助工具来诊断误差源。
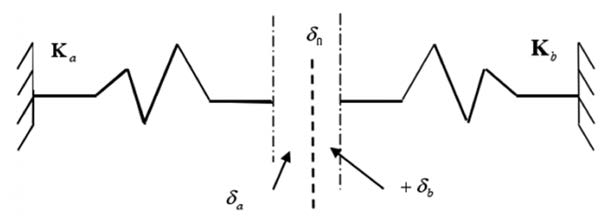
2.4柔性静态分析法
Merkley在1996年和1998年提出了可以预测装配力、应力和变形的柔性零件偏差分析方法,研究了材料和几何协方差与装配偏差之间的关系。该方法的特点是零件间接触点采用静态接触方式,在分析中将零件间的配合点视为静态接触,研究零件接触位置处的静态偏差,建立几何协方差和装配材料与装配偏差的关系,可预测装配应力、装配力和装配变形。如图13所示。
图 13 静态接触弹簧模型
材料协方差是由于接触弹性耦合产生的,可以利用零件的刚度矩阵得到。几何协方差与零件形状有关,通过零件表面轮廓得到。Stout应用多项式表征零件表面来计算零件的几何协方差。Bihlmaier提出通过光谱分析方法替代蒙特卡洛算法的光谱静态分析方法,该方法较柔性静态分析方法效率更高。
2.5一维偏置臂梁单元
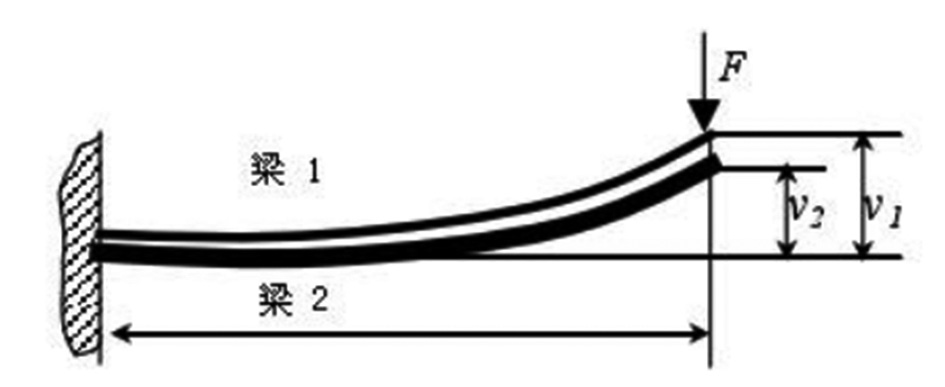
Liu于1995年提出一维偏置梁单元模型(如图14所示)。
图 14 一维悬臂梁单元模型
在该模型建立过程中Liu研究了悬臂梁焊接过程,采用偏置单元法对两个的厚度不同,自由端初始偏差分别为1v和2v的悬臂梁焊后偏差进行运算。
在分析过程中忽略焊接热应力作用,仅考虑焊点的力学性质对薄板件变形的影响,分析结果与实际出入较大。
2.6基于遗传算法的偏差优化模型
GM公司在1997提出了一种柔性件算法(如图15所示)。该算法以最小装配偏差为目标函数,结合统计评价和弹性静力学,使用遗传算法对装配工艺进行仿真与优化。
图 15 偏差优化模型流程图
该模型用性能指标S评价装配质量,将S在均值处进行泰勒级数展开为:
一维偏差分析和三维偏差分析
日本学者Takezawa根据对车身柔性钣金件焊接装配测量数据的分析,认为车身柔性薄板的装配偏差可能小于零件偏差,且接近于刚度较大的零部件偏差,开启了柔性薄板件装配偏差分析的先河。美国密歇根大学结合有限元和统计理论,对轿车车身柔性件装配偏差进行系统性理论研究,考虑钣金件易变形的特征,基于有限元法对焊接过程进行建模分析。主要的焊接装配偏差计算模型有一维偏置梁单元模型、偏差流模型、力学偏差模型。
1、一维偏差分析
一维偏差分析通过模拟零件在单一主线方向下的平移及尺寸偏差来建立数学模型,用以分析最终的配合公差。这种方法建模简单,分析迅速,能够快速地得到想要的分析结果。
传统的一维和二维公差模型是最早和最常用的公差分析方法;1974年,Evans给出了其数学关系式,即:
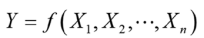
(6)
其中,Y代表功能要求或封闭环,Xi代表组成公差。
对式(6)的各组成环直接求导,即可得到极值条件下和统计条件下的公差累积函数:
式中,称为组成公差的敏感系数,代表了某一组成公差的变动对封闭环的影响程度,是公差优化和分配的重要参考依据。
在式(6)的基础之上,衍生了许多更为实用的方法,典型的有线性方法(Linearizationmethod)、系统矩(Systemmoments)、求积(Quadrature)、可靠性指数(Reliabilityindex)、田口方法(Taguchimethod)等。线性方法即最为常见的线性尺寸链方法。
在系统矩方法中,采用均值(Mean)、标准差(Standarddeviation)、偏度(Skewness)和峰度(Kurtosis)四个参数来描述偏差的分布情况。经过计算,可以得出封闭环的前四阶矩。这种方法能处理非正态分布的偏差。
求积法通过对组成环的密度函数求积分,得到封闭环的各阶矩:
(9) 式中,E[Yk]为Y的k阶矩;w(Xi)为组成环公差的概率分布密度函数,uXi为均值。可以看出,求积法完全基于数学推导,易于实现程序化。
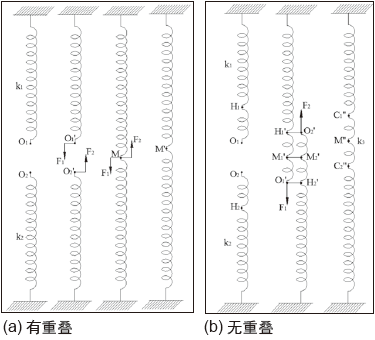
1.1基于一维弹簧结构的搭边回弹影响模拟
如下图16所示,两根一维弹簧无重叠(无搭边)拉伸装配。弹性系数分别是和而且,在弹性限度内分别由力和拉伸和到M处对接并固结,后释放拉伸力,弹簧产生回弹,固结点M偏离。理论过程表示为:
如式(14)所示,固结点M偏移至M'的位置与弹簧的弹性系数及固结点的M位置有关,与其他因素无关。
将两根弹簧重叠(搭边)进行拉伸装配。弹性系数分别是k1和k2,且k1≠k2。在弹性范围内由力F1拉伸到O'1到O'2后固定,形成一部分重叠区域
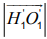
,且
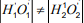
。假设形成重叠区的弹性系数,则有
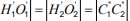
。释放拉伸力,弹簧产生回弹。理论过程表示如下;
如式(19)所示,回弹不仅与弹簧的弹性系数及固结点M的位置相关,还与重叠区的几何因素相关。式(10)与式(14)比较,参量A即为重叠区域对回弹偏离的影响。
综合以上理论分析,弹性件重叠区域对回弹量是有影响的,且与重叠区域的几何因素相关。
尺寸偏差分析技术发展展望
现在中国工业软件市场上,有80%的设计软件、制造软件、服务软件被国外品牌所占领使用,其核心技术部分,大多数都被国外巨头掌握,国内工业软件只能在夹缝中生存。就目前国内外的三维设计软件主要有来自美国PTC公司的高端Pro/E,美国UGS公司的高端UG和中端Solidedge,法国Dassault公司的高端CATIA和中端Solidworks,以及Autodesk公司的Inventor。目前在偏差分析领域,主流的尺寸偏差分析软件3DCS、VSA、CE-Tol6Sugma等均能做到与上述三维设计软件的无缝集成。伴随三维设计软件的推广应用,三维尺寸分析软件近五年在国内汽车、航空航天、机械等行业亦得到了推广和普及。
对于中国工业来说,工业软件是短板。伴随着数字化、网联化和智能化的深入发展,中国正在向智能制造迅速转型。中国制造业缺少核心工业软件,将是中国制造业的最重要的资源——“稀土”,缺少了就营养不良。
工信部自2015年提出“中国制造2025”发展战略之后,稳步推进智能制造落地,先后在标准体系、信息安全、试点示范项目等方面发布了专门的政策文件,极大地促进了我国智能制造和工业软件领域的发展。在智能制造发展规划中明确提出到2020年的量化目标,给出了企业和行业应用工业软件的路线图和时间表。工信部和国标委联合发布《国家智能制造标准体系建设指南》,为解决智能制造发展中的标准缺失、滞后以及交叉重复等问题起到了基础性和引导性作用。工信部先后公布三批智能制造试点示范项目名单,智能制造试点工作的推进将给工业软件的应用带来进一步的促进作用。
尺寸偏差分析智能优化方法国内发展与国际水平相当,国内外目前暂无成熟商用产品,均主要集中在企业、高校研究探索阶段。这也为国内研究人员提供了良好的赛道,建立尺寸智能优化方法,结合AI大数据、云计算等技术,实现尺寸设计方案、设计参数值最优化,提高优化过程的效率及可靠性,在未来十年内将大有作为。
作者:马振海,泛亚汽车技术中心有限公司
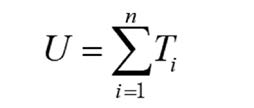
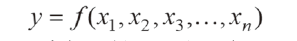 (1)
(1)


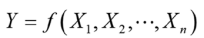 (6)
(6)
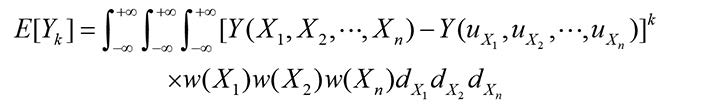

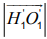 ,且
,且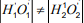 。假设形成重叠区的弹性系数,则有
。假设形成重叠区的弹性系数,则有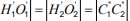 。释放拉伸力,弹簧产生回弹。理论过程表示如下;
。释放拉伸力,弹簧产生回弹。理论过程表示如下;
