三螺杆挤出机混炼性能评价及流场作用机制研究（下）

3. 基于流场模型的混合机制

经对TTSE的流场的分区计算，建立了流场特性参数理论模型。通过代入实验设备的几何参数及工艺参数，可以实现对设备剪切速率及拉伸速率的定量评估和预测。而流场的剪切速率和拉伸速率是决定混合效果的关键因素，大量研究证明分散混合效果与流场的剪切或拉伸作用强度存在定量关系[16-19]。因此，利用流场理论模型对设备分散混合效果进行预测，能够对特定物料的共混工艺进行针对性设计，完成对分散混合效果的参数化调控。此外，共混加工的理论计算条件与物料实际经历过程存在一定差异，通过对共混效果的预测评估和实验验证，有助于证明模型的可靠性，也便于分析模型误差产生的原因。

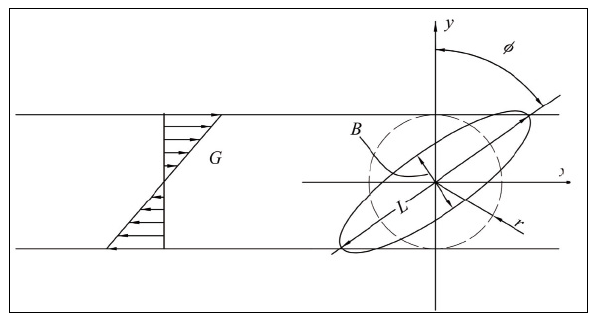
图1 0 分散相液滴变形破裂示意图

3.1 聚合物多相体系分散混合原理

流场特性对分散混合效果具有重要影响，众多研究试图建立流场剪切强度与分散相尺寸的定量关系。Grace[20]提出在不相容体系混合过程中，剪切作用将流体液滴由球形拉伸成为椭球形，如图10。并认定该条件下液滴的形变量为：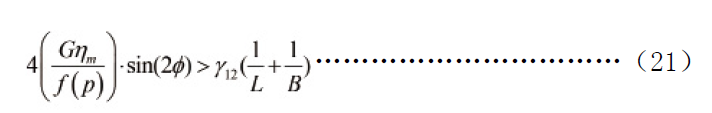



其中L和B为椭球体的长、短轴。随着液滴持续变形，当形变量达到流场的界面张力参数临界值（Eb）时，如式（22），椭圆形液滴发生破裂。



式中，G在本节代表流场剪切速率，r为分散相液滴的初始半径，ηm为流场连续相黏度，γ在本节指两相界面张力，f(p)为有关流场黏度比（p = ηd/ηm）的函数，ηd为分散相黏度，如式（23）所示。



在Grace的研究中，分析了流场条件对临界破裂尺寸影响，提供了一系列经验数据。吴守恒基于这一理论，在研究橡胶增韧塑料基体的过程中，建立了物理意义更为明确的分散相液滴破裂条件，即当流场对液滴的作用力大于两相界面应力时液滴破裂发生，如式（24）所示[21]。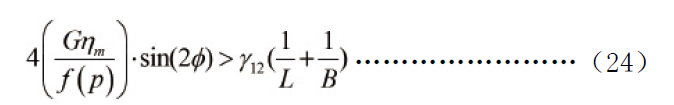



式中，φ为椭球体与流体流动切向的夹角，γ12为两相界面张力。

基于上述分散混合原理，聚合物熔体在流场中会不断变形破裂，直到液滴受到外界作用力不超过界面应力。因此，当流场剪切作用撤除后，椭球形的液滴将会恢复到球体，此时球体的直径则为分散相最小粒径。对于连续混合设备，物料在经历流场的混合作用后挤出定型，共混相形态与分散相粒径主要受各区域剪切作用水平影响。即使拉伸作用对分散混合效果同样具有重要影响，但由于在三螺杆连续混合过程中，中心区拉伸作用受局部压力场、充满度等因素影响较大，按理想状态计算得到的拉伸速率范围与实际情况存在一定误差。因此，本节通过TTSE流场理论模型，计算得到剪切速率分布，从而对PPO/PA66（30/70）体系进行分散相形态进行预测，并通过PPO/PA66的共混实验验证分析模型的可靠性。

3.2 PPO/PA66分散相粒径预测计算

3.2.1 实验材料及工艺

理论计算及相关参数测定所用共混体系为PPO/PA66（30/70），其中：

聚苯醚（PPO）：牌号LXR045，特性黏度为0.45±0.2 dL/g（氯仿，25℃），蓝星化工新材料股份有限公司生产；

聚酰胺66（PA66）：牌号EPR27，相对黏度2.67，平顶山神马工程塑料有限责任公司生产。

根据PPO、PA66对加工温度和设备扭矩的要求，设定TTSE螺杆转速为200 r·min-1，物料的加工温度为280℃，在此工艺条件基础上进行预测计算。

3.2.2 三螺杆挤出机流场剪切速率分布

表5 三螺杆挤出机流场几何参数

由于TTSE流场各区域剪切速率水平不同，因此在粒径预测计算中，利用各区域剪切速率的边界值计算该区域分散相最大及最小粒径，以便评估整个流场分散相粒径水平。实验用TTSE几何参数，如表5所示。螺杆在200r·min-1下，流场各区域的剪切速率范围，如表6。

表6 三螺杆挤出机流场剪切速率分布

3.2.3 PPO/PA66体系黏度场

聚合物基体PA66的黏度由毛细管流变仪（Polylab OS，HAAKE）测得，根据TTSE流场剪切速率预测结果，设定螺杆转速与加工温度（280℃），获得四组黏度曲线，如图11。四组曲线在修正拟合后，获得PA66的剪切黏度曲线。

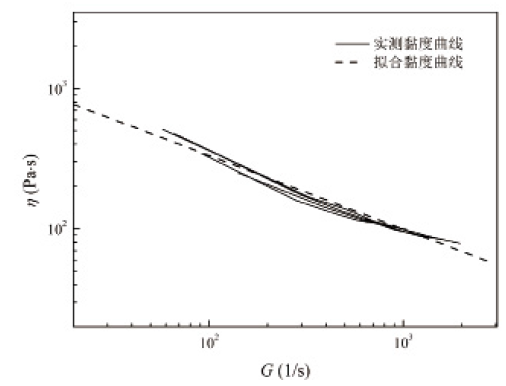
图11 PA66剪切黏度曲线拟合

分散相PPO的黏度极高，无法通过毛细管直接挤出测得表观黏度。因此，采用平行平板（直径20mm）旋转流变仪（MARS III，HAAKE）在280℃氮气气氛下，测得试样品的复数黏度（complex viscosity），而后经Cox-Merz理论[22]换算后获得PPO表观黏度（apparent viscosity）数据。由于TTSE流场剪切速率值较高，而旋转流变仪频率扫描模式下，最大剪切速率仅为100s-1，无法覆盖全部的理论计算范围。因此，首先以频率扫描模式测得280、290、300、310℃四个温度的PPO复数黏度曲线，而后通过时温等效计算获得剪切速率与PPO黏度关系主曲线（图12）。

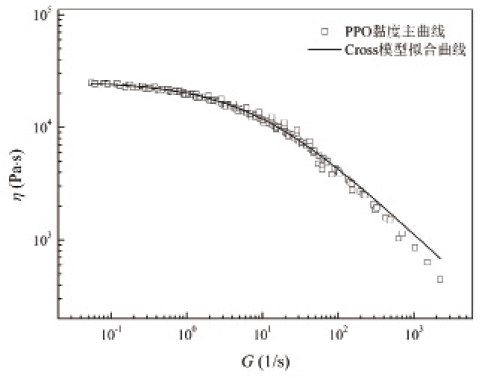
图12 PPO剪切黏度主曲线及Cross模型拟合曲线

对PPO剪切黏度主曲线进行Cross模型拟合以便计算不同剪切速率下的分散相黏度，模型如式（25）所示。



其中，η0为零切黏度，λ为松弛时间，n为非牛顿指数。η0可通过流变仪的蠕变实验得到。经拟合计算，PPO在280℃下的Cross模型主要参数，如表7所示。

表7 PPO在280℃下的Cross模型参数

通过上述测试，获得PPO与PA66在表6剪切速率范围内的黏度数值及黏度比相关参数，如表8所示。

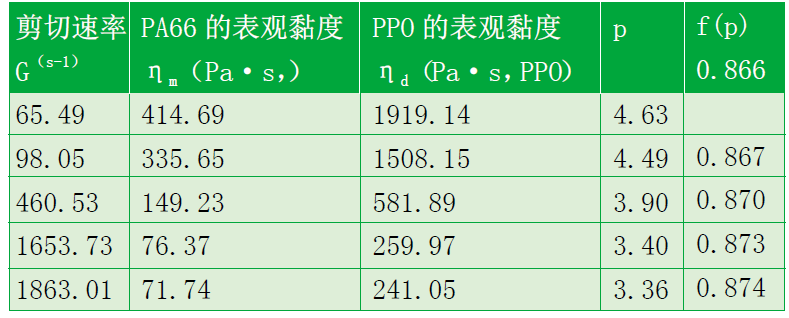
表8 PPO、PA66黏度值及相关参数

3.2.4 PPO/PA66共混体系分散相粒径计算

模型中两相的界面张力γ12（interfacial tension）的测算，基于经典的界面张力计算公式[21]：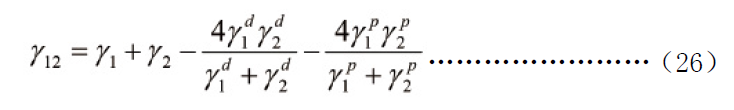



式中γ1和γ2分别代表PPO和PA66的表面张力（surface tension），γd和γp代指表面张力的非极性（nonpolar）和极性（polar）部分，在此利用测量聚合物固体表面接触角的方法获得。

由于材料的表面张力随温度变化，因此预测模型计算过程中，两相界面张力的计算应使用加工温度下物料的表面张力。而在聚合物熔融温度下，难以通过接触角实验测得材料表面张力的极性部分。由于材料表面张力极性部分占比为χ，该值不随温度变化，即：



因此，利用表面张力仪（DCAT21，Dataphysics）测得常温下PPO与PA66的χ值，及加工温度下材料的表面张力，如表9所示。式（26）中代入相关参数，即获得到PPO/PA66体系界面张力γ12为5.75mN/m。

表9 PPO与PA66的表面张力参数

此外，在图2-8的模型中，变形后椭球体的L和B，及sinφ也是影响最小粒径的重要参数。Grace认为共混物的分散相液滴破裂前，其临界形变尺度直接与两相黏度相关，并利用实验确定了p与(L-B)/(L+B)的定量关系曲线[20]。因此，根据表8中p值即可确定L/B（表10）。

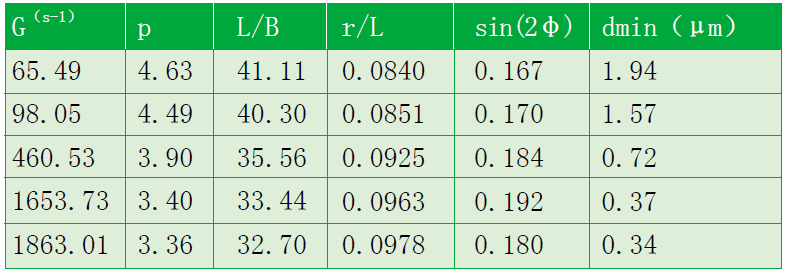
表10 PPO/PA66体系形变参数及最小粒径

在液滴形变过程中，椭球形的长轴与球型近似形成直角三角形，如图10所示。而由于分散相液滴破裂前，球体与椭球体体积相等，如式（2-29）。因此，通过代入L/B值即可确定球体半径r与L的比值，从而计算得到sin(2φ)。



最终，基于式（24）的液滴破裂模型，通过上述形变参数与表6、8、9中流场特性参数，即可得到PPO/PA66两相共混物在计算工艺条件下的最小颗粒直径dmin，如表10所示。

3.2.5 PPO/PA66分散相粒径预测的实验验证及误差分析

根据TTSE流场理论模型的计算结果，已实现PPO/PA66两相共混物分散相颗粒直径的预估分析。而为了确定该预测方法的可靠性，需要进行相同条件下对比实验。并通过多工艺下的PPO/PA66体系共混，对存在的误差进行分析，以便指导后续高性能PPO/PA66制备研究。

3.2.5.1 PPO/PA66共混样品制备及表征

在共混加工前，将PPO、PA66置于真空干燥箱，80℃干燥12小时。而后将PPO/PA66按30/70的比例称量，利用高速搅拌机预混。将预混后的共混物加入TTSE（自制，螺杆直径D=35.2 mm，L/D=28），由加料口到机头温度由240℃逐渐升高至280℃，产量设定为10 kg·h-1。制备三组样品用以验证及误差分析，螺杆转速设定为100、200、300 r·min-1，待设备稳定挤出1kg以后由机头取挤出样条5份。

图13 三螺杆挤出机共混PPO / PA 66 ( 30 / 70 )体系SEM照片

将样条置于液氮充分冷冻，取出后快速脆断。而后，将样条断面浸泡于氯仿中8小时，用于溶解刻蚀PPO相，以便分散相形态的观察。将样条断面干燥并进行喷金处理，利用HITACHI-S4700扫描电子显微镜（SEM）拍摄共混物相形态照片。

利用图片处理软件（Image J 1.41）计算共混物分散相粒径及粒径分布，每组样品统计粒子总数为300-500个，数据用于绘制粒径分布直方图。

利用平行平板旋转流变仪（Mars III，HAAKE，平板直径20mm）测得材料的相关动态流变曲线。测试条件为：平板间隙1mm，频率扫描下控制应变1%，测试应变下熔体处于线性黏弹区范围内。

3.2.5.2 实验结果及讨论

图13为PPO/PA66体系经TTSE以200 r·min-1转速共混后的SEM照片。由共混物分散相粒径分布图（图14）发现，分散相粒径主要集中于0.7~2.3μm范围（占比达2.5%以上的粒径区段），部分区域出现较小粒子，粒径可达预测最小值0.34μm左右。预测粒径分布（图14）根据各区域面积加权统计。通过实验与预测值对比，预测分布与实际分布对应较好，证明了理论计算能够较准确预测分散相粒径分布范围。

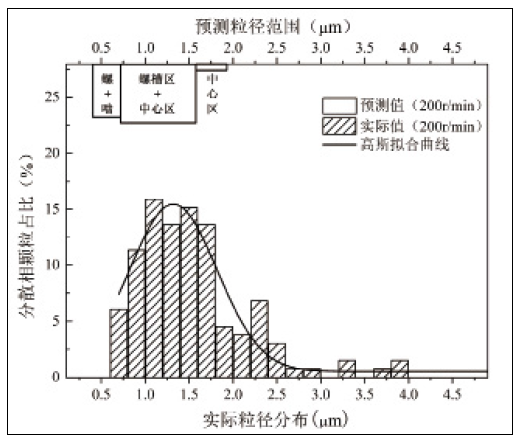
图14 三螺杆挤出机制备PPO/PA66(30/70)体系分散相粒径分布图

通过对比发现，实测粒径集中分布区间与螺槽区（除螺棱）、中心区的预测值（0.72~1.94μm）最为接近。一方面，这是由于螺槽区与中心区在流场中占据较大范围，中心区与螺槽区占流场横截面积约94%，因此该区段的剪切速率水平决定了共混物中分散相粒径的分布范围。另一方面，在啮合区与螺棱处剪切速率较高，同时由于流道狭窄形成了较高的局部压力，因此物料不易进入这一区域。同时，实验样品的分散相有约15%的粒子直径大于理论最大值。这一现象可能是由于TTSE流场剪切作用较强造成聚合物降解所致。在TTSE挤出共混过程中，物料经历多次强烈的剪切作用会造成流场局部温度上升，从而导致PA66降解，两相黏度比大于计算值，分散相粒径预测结果也因此误差增大。此外，TTSE较强的剪切作用也会导致PA66分子发生链断裂，黏度进一步降低。因此，为了验证误差产生的原因，需要对不同转速下的PPO/PA66分散相粒径进行预测与验证，以分析误差产生的原因。

3.2.5.3 误差分析及验证

通过预测值与实验值的对比发现，PPO/PA66共混物在实际挤出加工后，部分分散相粒径超出理论计算最大值。根据PA66基体的材料特性，推测可能由于TTSE部分区域的高剪切速率使其降解，从而增大了体系黏度比，不利于分散混合。因此，通过增加100·min-1和300 r·min-1的对比组，验证误差产生的原因。不同螺杆转速下流场的理论剪切速率及粒径预测值，如表11所示。

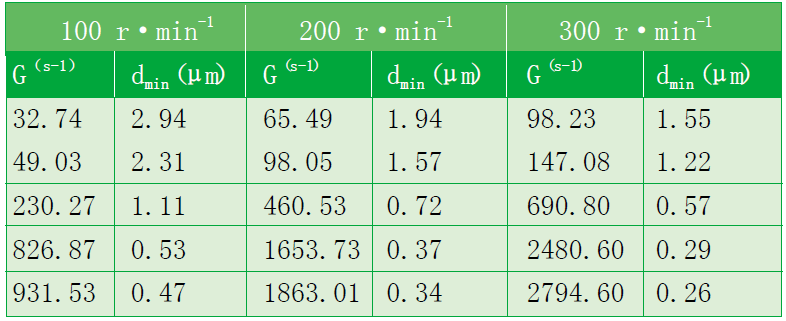
表11 不同螺杆转速下PPO/PA66体系粒径的预测值

图15为各螺杆转速下的PPO/PA66共混物的SEM照片，图16为对应的粒径分布图。结合图13与图15，对比100~300 r·min-1三组转速下加工的PPO/PA66共混物样品，分散相粒径在转速提升到200r · min-1时有所下降，但当转速提升至300 r·min-1时，粒径并未有明显的减小。通过将实际共混物粒径集中分布区间与理论预测的集中分布区间（中心区与螺槽区）进行对比，如表12所示。

图15 不同螺杆转速下PPO/PA66(30/70)共混物SEM照片

在100 r·min-1转速下，预测值粒径分布与实际共混物粒径最为接近，此时剪切较弱，材料结构和物性稳定，因此误差最小。但其实际粒径集中分布范围（0.9~2.7μm）略小于理论预测值（1.11~2.94μm），说明在剪切作用有限时，基于剪切场的预测具有局限性，拉伸作用能够使分散相粒径进一步减小，因此实际粒径更小。而对于螺杆转速为300 r·min-1下的共混物，预测值（0.26~1.55μm）与实际值（0.7~2.1μm）误差较大，虽有部分粒子接近理论最小粒径，但却有大量分散相粒子直径大于理论最大值。造成误差产生的原因很大可能是由于螺杆转速升高带来的更的强剪切作用，同时使流场内局部温度波动增大，而PA66基体在强剪切和高温作用下易发生降解，从而使共混物两相黏度比增高，导致分散相粒径大于预测值。

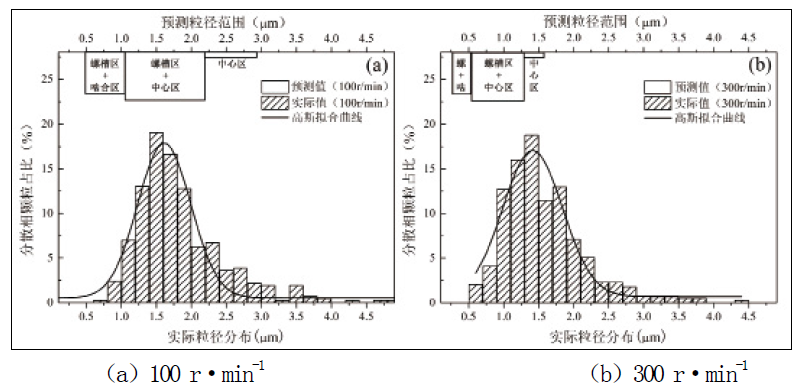
图16 不同螺杆转速下PPO/PA66共混物分散相粒径分布

为进一步论证误差产生的原因，并定量研究聚合物基体降解程度，分别对PPO和PA66进行单独挤出加工，以确定热历程对两相黏度比的影响。由于PPO黏度较高，难以分别在100、200、300 r·min-1下进行挤出实验。因此仅选用适宜的加工转速挤出后，与未经加工的PPO原粉一同进行流变测试，如图17所示。在经热历程后，PPO的黏度不但没有下降，反而出现一定程度升高。这可能是由于PPO分子链在热历程中发生偶合而使其分子量提升，从而使加工后样品熔体黏度增大。

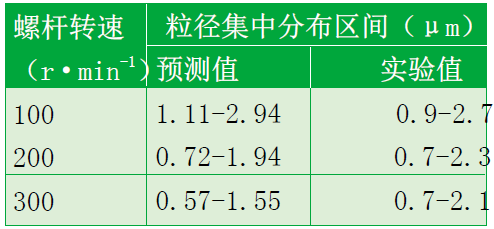
表12 PPO/PA66共混物粒径集中分布区间预测值与实验值

PA66由于黏度较低易于加工，分别在三组实验转速下挤出，其黏度曲线如图18所示。通常，聚合物在低频区的粘弹性反映了分子链的运动与松弛特性，PA66的低频区黏度随螺杆转速升高大幅下降，说明强剪切作用造成了分子链发生断裂，分子量下降，证明PA66基体发生一定程度的降解。但高频区内，PA66黏度因螺杆转速升高同样不断下降。结合PPO黏度在经热历程后增大的现象，证明了在PPO/PPA6共混过程中，两相黏度比将随螺杆转速的升高而增大，这将不利于PPO相的分散及混合，同时也造成了预测值与实际值间存在误差。

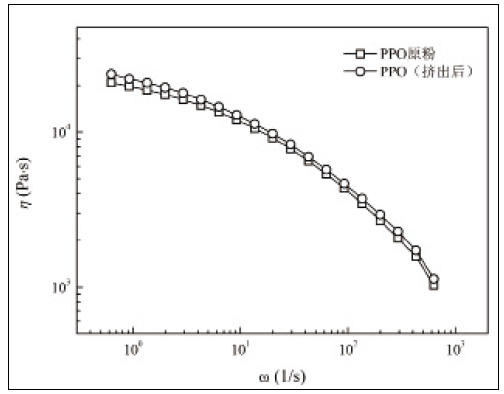
图17 PPO加工前后的黏度曲线

而根据经热历程后的PA66黏度曲线，对300 r·min-1的粒径分布进行修正后，预测粒径集中分布区间为0.72~2.24μm，实际粒径集中分布区间则为0.7~2.1μm，实际值与预测值之间误差显著减小。而由于预测值略大于实际值，说明可能由于拉伸流场的存在，促进了分散相粒径不断减小，使实际粒径水平较基于剪切流场的预测值更低。

4.结论

混炼设备流场的剪切及拉伸速率是影响混合效果的关键因素。而对于三角形排列三螺杆挤出机（TTSE），尚未有相关论述建立定量评价其流场剪切速率和拉伸速率的方法。本文通过对TTSE流场进行分区简化，确立了各区域流道模型，并基于此建立了TTSE流场特性参数模型，实现了对于该流场内剪切或拉伸速率的定量计算。通过对流场的分区处理，提高了剪切或拉伸速率计算的准确性，为流场混合效果的参数化调控和评估建立了理论基础。

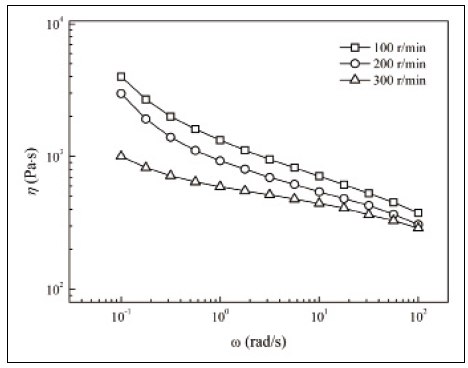
图18 不同螺杆转速加工PA66的黏度曲线

基于TTSE流场理论模型，利用聚合物分散混合理论，实现了对三螺杆挤出共混PPO/PA66体系分散相粒径分布的预测。并通过共混实验，证明了该预测方法及流场理论模型的可靠性。该预测方法的建立有助于评估设备的混合能力，并对共混工艺的设计具有一定参考意义，为共混效果与材料微观结构关联的研究奠定了基础。

研究表明，由于TTSE流场内强剪切作用区域较多，过高的转速会造成热稳定性较差的PA66降解，从而影响该预测方法的准确性。这一现象也说明，对于聚合物共混体系，选择合理的工艺及设备有助于获得更好的共混效果。而经修正后，实际值均小于预测值，说明可能由于拉伸作用存在造成粒径进一步减小。

参考文献

[1]    王国全. 聚合物共混改性原理与应用[M]. 中国轻工业出版社, 2007.

[2]    陈怡, 刘廷华. 多螺杆挤出机的开发与应用进展[J]. 中国塑料, 2004, 18(6): 17-20.

[3]    Y Suzaka. Mixing device[P], U.S. Patent. 4334783, 1982

[4]    LA Utracki, A Luciani, DJ Bourry, Extensional flow mixer[P], U.S. Patent. 6550956, 2003

[5]    刘钵. 拉伸流场中成型高强度PP/HDPE合金的性能与形态结构研究[D]. 四川大学, 2006.

[6]    黄磊. 拉伸流场对聚烯烃/纳米CaCO_3填充体系的分散混合作用[D]. 四川大学, 2007.

[7]    Meissner J, Hostettler J. A new elongational rheometer for polymer melts and other highly viscoelastic liquids[J]. Rheologica Acta, 1994, 33(1): 1-21.

[8]    瞿金平，基于拉伸流变的高分子材料塑化输运方法及设备，中国发明专利，CN 200810026054.X, 2010

[9]    庞军舰. 三螺杆挤出机混合特性的数值模拟和实验研究[D]. 北京化工大学，2012.

[10]    庞军舰, 何亚东, 信春玲, 余东泉, 李庆春. 三螺杆挤出机螺杆元件混合特性的数值研究.中国塑料, 2012, 26(1): 103-108

[11]    Yang K, Xin C, Yu D, et al. Numerical simulation and experimental study of pressure and residence time distribution of triple-screw extruder[J]. Polymer Engineering & Science, 2014, 55(1):156–162.

[12]    朱向哲, 谢禹钧, 苗一. 三螺杆挤出机常规螺纹元件挤出过程的CAE研究[J]. 塑料工业,2004,09:29-32.

[13]    朱向哲, 谢禹钧, 苗一. 三螺杆挤出机中胶料流动的三维流场分析[J]. 轻工机械,2004,04:29-31.

[14]    张文呈, 姜南, 信春玲. 母粒制备中三螺杆挤出机的填充和分散效果分析[J]. 塑料,2007,04:1-4+31.

[15]    张伟. 同向三螺杆挤出机的混炼性能评价[D]. 北京化工大学, 2011.

[16]    Harold P G. Dispersion phenomena in high viscosity immiscible fulid systems and application of stastic mixers as dispersioni devices in such systems[J]. Chemical Engineering Communications, 1982, 14: 225-277.

[17]    Chris E Scott, Christopher W. Morphology development during the initial stages of polymer-polymer blending[J].Polymer, 1995, 36(3): 461-470.

[18]    J. M. H. Janssen， H. E. H. Meijerentre. Droplet breakup mechanisms: Stepwise equilibrium versus transient dispersion[J], Journal of Rheology, 1993, 37: 597-608

[19]    John K., Theodore G. S, David I. B. Study of Breakup Mechanisms in Cavity Flow[J]. American Insitute of Chemical Engineers, 1996, 42: 649-659.

[20]    Harold P G. Dispersion phenomena in high viscosity immiscible fulid systems and application of stastic mixers as dispersioni devices in such systems[J]. Chemical Engineering Communications, 1982, 14: 225-277.

[21]    Wu S. Formation of dispersed phase in incompatible polymer blends: Interfacial and rheological effects[J]. Polymer Engineering & Science, 1987, 27(5):335-343.

[22]    Cox W P, Merz E H. Correlation of dynamic and steady flow viscosities[J]. Journal of Polymer Science, 1958, 28(118):619-622.