空气压缩机 | 如何选择气体压缩机

考虑到工艺要求（从负载曲线中得到的平均空气消耗量），适当的裕度和系统中的摩擦损失，以及空气湿度而要做流量校正，在吸入状态下，压缩机的流量必须达到720m3 / h。为了满足消费者的要求，应以0.83MPa的压强，在干燥、无油的环境下输送压缩空气。可用电流频率为60 Hz。

工作条件

吸气工况下的输送能力(Qs) = 720 m3/h

吸入压力 (abs) (ps) = 0.101 MPa

吸入温度 (ts) = 30°C

相对湿度: 80%

排气压力 (abs) (pd) = 0.83 MPa

根据预期安装地点的历史天气记录来确定吸入温度和相对湿度值。

从数据表中得知空气性质为:

等熵指数(k) = 1.399

分子量(MW) = 28.97 kmol/kg

第一步是计算压缩机的等熵能头。为选择最合适的压缩机类型，应将计算所得的等熵能头值输入图8.1所示的图表中。为确定应使用哪个方程，需要找到吸气和排气工况下的压缩系数Zs和Zd。在这一步之前，必须得到排气温度。

排气温度：Td = Ts (pd/ps)(k-1)/k(1.21, part 1) ［2］

对于空气应用，可以认为等熵指数k在极为相似的压缩路径上保持恒定。如果需要更准确的计算，则应该获得k的平均值。

从空气特性表中可以找到压缩因子：

Zs = 0.9999

Zd = 1.0028

可以使用方程1.9 来计算等熵能头Ha：

Ha = 101.972 [k/(k-1)]

Z.R.Ts[(pd/ps)(k-1/k) –1]

Z = (Zs + Zd)/2 = (0.9999+1.0028)/2 =1.0013

R = 8.3142/MW[2]

R = 8.3142/28.97 = 0.287 kJ / kg K

Ha = 101.972 [1.399/(1.399-1)] 1.0013(0.287)(30 +273.15) [(0.83/0.101)(1.399-1/1.399) -1] =25,648.7 m

对于活塞式空气压缩机，等熵压缩可以得到良好的结果。

所需功率：

GKWa = w Ha / 367,200 (1.13)[2]w = Qs / vs

从焓湿图可知：

vs = 0.889 m3/kg

w = 720 / 0.889 = 809.9 kg/h

GKWa = (809.9)(25,648.7) / 367,200 =56.6kW

所需的主轴功率由下式计算得到：KW = GKWa / (ηm ηc) (1.19)[2]

根据表8.1中给出的参考数据，可以确定机械效率ηm= 0.880，另外通过图8.2所示曲线可以推断气缸效率ηc= 0.846。当我们在高压力比情况下处理达到大气压力的空气时，比重和入口压力的校正因子都等于1。

KW = 56.6 / (0.880)(0.846) = 76.0 kW

表8.1，空压机机械效率的通常范围。

压缩级数

上述计算得到的排气温度过高，所以必须找到一种替代解决方案，以达到较低的排气温度值。这个温度与压缩级数密切相关，所以最好同时处理这两方面的问题。

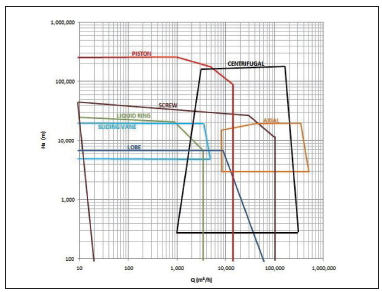
图8.1 压缩机类型选择图。

据表8.2所示，对于所提的工作条件，建议使用两级压缩机。这是一种方便的解决方案，它允许使用级间冷却，从而达到极低的最终温度。此外，它还具多级压缩的其他优点。

利用公式1.26 [2]计算理想条件下的中间压力px。

px = (pf . pi)1/2

考虑到在中间冷却器和分离器中会产生0.04MPa的压降，并且第二级的吸入温度将高于第一级的吸入温度，因此通过使两个压缩级的排气温度彼此相等，就能够获得很好的结果。通过数学变换得到以下表达式：

px = ((p1.p4 (T3 /T1)k/(k-1) + (Δp/2)2)0.5

其中P 4 = 第二级的排气压力（MPa），T3=第二级的吸入温度（K），Δp =压降（MPa）。

理想情况下，在进入第二级压缩之前，应使空气冷却到与首级压缩吸入温度相同的温度，即30°C。但这需要一台非常大型的级间热交换器，无论从技术还是经济角度来看，这都不是一种最为便捷的解决方案。因此，作为暂时的权宜之计，设定第二级压缩的吸入温度为42℃。 然后：

px = ((0.101 . 0.83 ((42 + 273.15) /(30 +273.15))1.399/(1.399-1) + (0.04/2)2)0.5 =0.311 MPa

首级计算

排气温度

T2 = T1 (p2/p1)(k-1)/k

p2 = px + (Δp/2) = 0.311 + (0.04/2) =0.331MPa

T2 = (30 +273.15) (0.331 / 0.101)(1.399-1)/1.399 =425.1 K = 152.0 °C

压头：

Ha = 101.972 [k/(k-1)] Z.R.T1 [(p2/p1)(k-1/k)–1]

从表中查得：

Z2 = 1.0009

Z = (0.9999 +1.0009)/2 = 1.0004

Ha = 101.972 [1.399/(1.399-1)] 1.0004(0.287)(30 +273.15) [(0.331/0.101)(1.399-1/1.399) – 1] =12,521.6 m

所需功率：

GKWa = w Ha / 367,200

GKWa = (809.9)(12,521.6) / 367,200 =27.6kW

从表8.1和图8.2中得知效率值为ηm =0.900，ηc = 0.881。

KW = 27.6 / (0.900)(0.881) = 34.8 kW

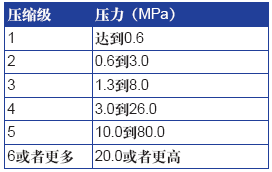
表8.2：活塞式空压机的排气压力。

二级计算

排气温度：

T4 = T3 (p4/p3)(k-1)/k

p3 = px - (Δp/2) = 0.311 - (0.04/2) =0.291MPa

T4 = (42 +273.15) (0.83 / 0.291)(1.399-1)/1.399 =425.1 K = 152.0 °C

如果在这种情况下使用平均等熵指数计算，则得到的排气温度将会低2°C左右。

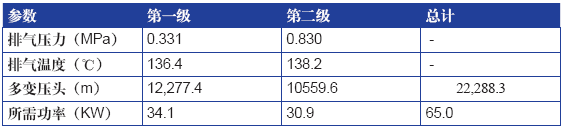
表8.3：考虑气缸强冷却（多变压缩）的所得计算参数，其中指数等于1.34。

压头：

Ha = 101.972 [k/(k-1)] Z.R.T3 [(p4/p3)(k-1/k) 1]

从表中得知：

Z3 = 0.9996

Z4 = 1.0024

Z = (Z3 + Z4)/2 = (0.9996 +1.0024)/2 =1.0010Ha = 101.972 [1.399/(1.399-1)] 1.0010(0.287)(42 +273.15) [(0.83/0.291)(1.399-1/1.399) -1] =11,296.4 m

所需功率：

GKWa = w Ha/ 367,200

为了使计算更准确，应确定在级间冷却器中冷凝并在分离器中被分离的那部分水的质量，以便从空气质量（w）中将其减去。

GKWa = (809.9)(11,296.4) / 367,200 = 24.9kW

考虑到本例中的空压机大小适中，压力比也是中等值，因此从表8.1中确定机械效率为ηm= 0.910。从图8.2中确定气缸效率取为ηc= 0.873。入口压力的效率乘数为0.9993。

KW = 24.9 / (0.910)(0.873)(0.999) = 31.4 kW

所需功率总量（两个压缩级）：

KW = 34.8 + 31.4 = 66.2 kW

该结果表明，在这种情况下，两级压缩的功耗比单级压缩低12.8%。

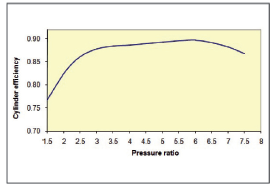
图8.2：活塞式空压机的气缸效率。

由于两个压缩级的排气温度均略高于150℃的极限值，因此建议对压缩过程中为了降低排气温度而采取的气体强化冷却措施予以评估。例如，通过对气缸的强化冷却，可实现指数达到1.34的多变压缩过程。表8.3中给出了应用该指数的对应结果和相同的计算程序。

通过强化冷却，使功率需求量降低了1.8％。然而这仅是冰山一角。由于气缸温度较低，可靠性得到提高，进而使成本降低，这样的结果带来了极为重大的好处。由于引入强化冷却措施使得初始投资成本和运行成本都有所增加，故应该通过LCC分析进行评估。